힙이란?
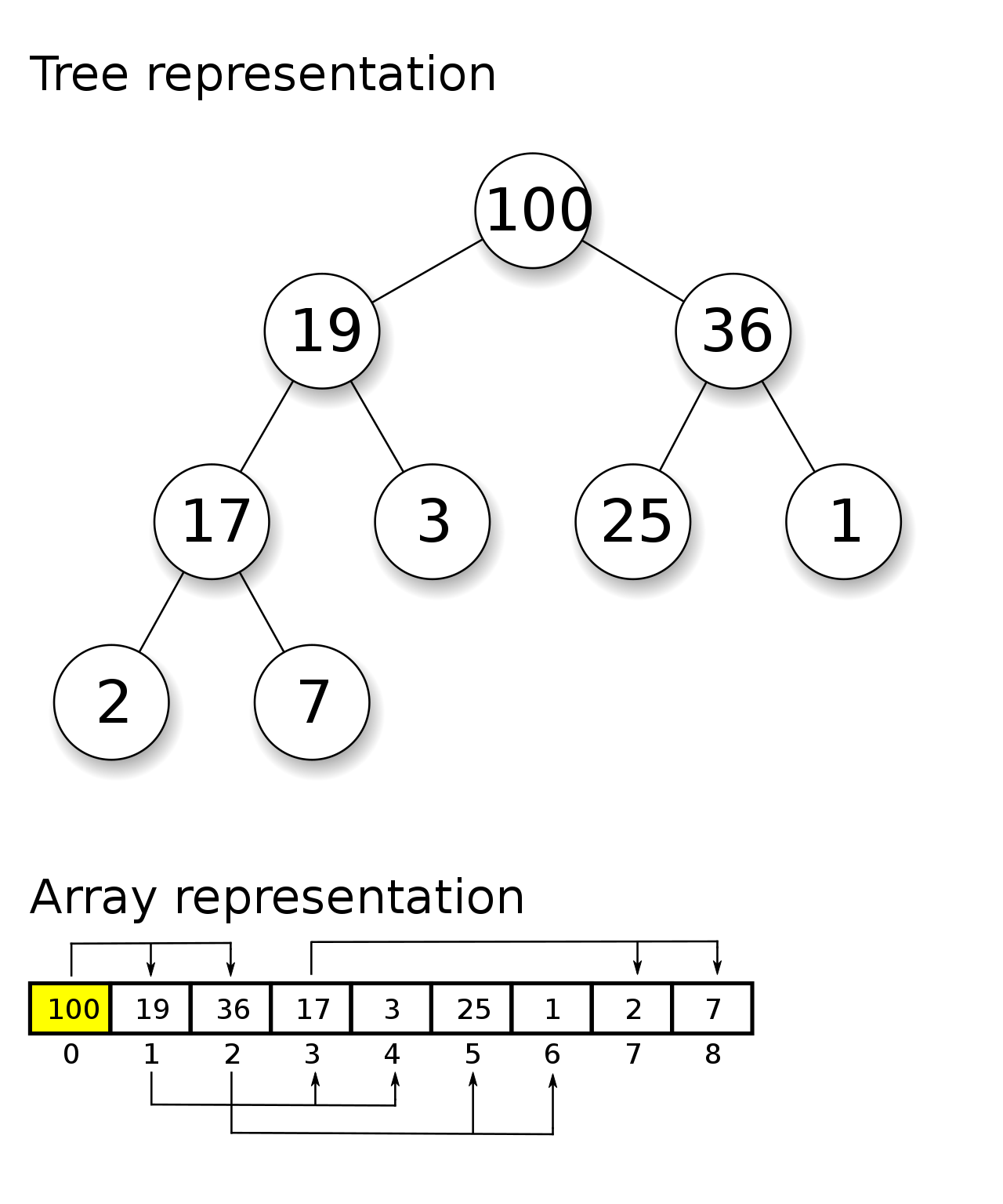
힙은 기본적으로 완전 이진트리(complete Binary Tree)를 기본으로 한 자료 구조이며, 부모 노드와 자식 노드 간의 대소관계가 성립하는 자료구조이다.
- Heap (힙): 상위 노드의 값이 하위노드(들)의 값과 관련하여 특정 방식으로 정렬되는 트리 기반 데이터 구조이다. 힙은 최소 힙(부모 노드의 값이 자식의 값보다 작거나 같음) 또는 최대 힙(부모 노드의 값이 자식의 값보다 크거나 같음) 일 수 있다.
최소 힙의 목적은 부분 순서가 있는 객체를 저장하는 것이다. 최소 힙에서 최소 객체를 제거하는 빠른(O(log n)) 방법이 있다. 최소 힙은 최소 계산이 여러 개 있는 계산에 유용하다.
힙에서 최댓값을 추출하는 최대 힙이라는 유사한 구조가 있다.
힙은 최대 힙 이거나 최소 힙이고, 동시에 둘이 될 수 없다. 최소 힙의 구현이 주어지면, 최대 힙은 요소 간의 비교를 뒤집음으로써 구현될 수 있다. 이후 나머지 부분에서는 최소 힙만 논의하기로 한다.
힙은 때때로 우선 순위 대기열(queue)라고 부르기도 한다. 기술적으로, 힙은 우선순위 대기열의 하나의 구현에 불과하다.
핵심 용어
키 : 순서를 결정하는 값. 숫자를 저장한다면 숫자가 키가 될 수 있다. 만약 더 복잡한 객체를 저장한다면, 키는 우리가 비교하는 데이터 필드이다. 해시 테이블(hash table)과 달리, 힙의 키는 고유할 필요가 없다.
최소 추출: 최소 힙에서 최소 요소를 (빠르게) 추출할 수 있는 방법
힙 속성 및 완전 이진 트리와 같은 힙에 대한 구현별 세부 정보가 있으며 힙을 처음부터 만드는 방법을 이해하는데 유용하지만 힙을 사용하여 인터뷰 문제를 해결하는 데는 그다지 유용하지 않다.
| 강점 | 약점 |
| 최소 힙 활용 가능 | 특정 키 값을 빠르게 찾을 수 없음 |
| 빠른 최소 값 추출 | 항목들이 부분적으로만 정렬됨 |
| 생성된 정렬된 배열 | 힙 속성을 적절히 활용하면 검색 과정을 일부 가지치기 할 수는 있지만 일반적인 효율적인 검색 방법보다는 느릴 수 있음 |
출처 : https://en.wikipedia.org/wiki/Heap_(data_structure)
Heap (data structure) - Wikipedia
From Wikipedia, the free encyclopedia Computer science data structure Example of a binary max-heap with node keys being integers between 1 and 100 In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: In a
en.wikipedia.org
https://evan-moon.github.io/2019/10/12/introduction-data-structure-heap/
최소 값과 최대 값을 빠르게 찾을 수 있게 도와주는 힙(Heap)
이번 포스팅에서는 대표적인 자료 구조 중 하나인 에 대한 설명과 구현을 한번 해보려고 한다.
evan-moon.github.io
'Data Structure' 카테고리의 다른 글
| [Data Structure] 자료구조란? (0) | 2023.08.07 |
|---|---|
| [Python] Linked List vs. Array (0) | 2023.08.07 |
| [Data Structure] 데이터 표현 방법 (Data representation) (0) | 2023.08.07 |


